研究とは新しい分野を作ること－複雑ネットワークの新発見と非エルミート量子力学の開拓｜羽田野直道

「未然課題」連続インタビュープロジェクト

インタビュー#16　羽田野 直道

東京大学生産技術研究所 教授｜量子熱・統計力学

物理の一分野である量子熱力学と統計力学を専門とする羽田野直道氏は、さまざまなテーマの研究に取り組み、新しい分野の開拓に挑戦されています。
今回のインタビューでは、統計物理学の最新テーマの1つ「複雑ネットワーク」と、量子力学の最新テーマの1つ「非エルミート量子力学」についてご紹介いただきました。

人やものがつながる複雑ネットワークの研究

物理学の究極の目的は普遍的な法則を見つけることです。通常扱う自然界だけでなく人間の行動ですら、数学を道具として記述し、その中から統一的な法則を発見するのが物理の目指すところです。なかでも、一見、全く異なるように見えるものを解析し、そこに共通の性質があることを発見するとわくわくします。私の研究室で取り組んでいる複雑ネットワークの解析はそのような研究の1つです。
物理では点と線を結んだものを「ネットワーク」と呼びます。人やもの同士のつながりも「ネットワーク」です。近年の研究で、世の中に実在するネットワークの多くが、それまで数学で扱われていたようなランダムなネットワークとは全く異なる統計的性質を持っていることが明らかになってきました。それらを総称して特に「複雑ネットワーク」と呼んでいます。
我々を取り巻く世界にあるネットワークには、ハブやコミュニティー（クラスター）が存在します。与えられたデータのみからコミュニティーを検出することは難しく、長年研究が進められてきましたが、私の研究室では、後述する方法を用いて、効率的にコミュニティーを検出することに成功しました。
複雑ネットワークの一例に「ザッカリーの空手クラブ」というものがあります。ザッカリーはアメリカの社会心理学者で、ある大学の空手クラブの部員を対象に交友関係を調べました。質問は2つあり、1つ目は「あなたは誰と友達か」というものです。その結果を線で結ぶと図1のようなネットワークを描くことができます。大きく分類すると、1番を中心とするグループと34番を中心とするグループに分かれていることがわかります。
実は1番がこの空手クラブの部長、34番が師範です。この2人は仲違いをしてしまい、その結果、空手クラブが2つのグループに仲間割れしてしまいました。その2つのグループを当てるというのが、コミュニティー検出の研究で練習問題としてよく用いられるのです。というのは、ザッカリーは同時に「あなたは部長派ですか、師範派ですか」という質問をしているので、コミュニティー検出手法の答え合わせができるからです。

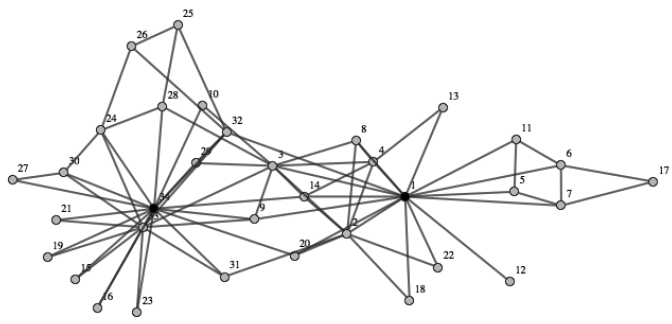
図1 「ザッカリーの空手クラブ」での友人関係のネットワーク

ネットワークのコミュニティーを検出する

次にこのザッカリーの空手クラブのデータを、私が専門としている統計力学の手法を用いて整理してみます。簡単に言うと、部員同士の直接的なつながりだけでなく、間接的なつながりにも重みづけしながら計算に取り入れるという方法です。
例えば図2のようなネットワークを考えましょう。AとBは最短2ステップでつながり、AとCは最短3ステップで結ばれています（赤線部分）。従来の解析手法では、最短何ステップで結ばれているかを重視し、それ以外にどのようなつながりがあるかは無視されていました。

図2

しかし、AからCまでは3ステップ以上の経路が何本もあることがわかります（青線部分）。この場合、AとCは、AとBより距離は遠いものの、必ずしも結びつきが弱いとは言えません。そこで私の解析手法では、最短の経路だけではなく、それより長い経路が何本あるかも無視せずに取り入れます。その道のりの長さに応じた重みを付けて足し算し、AとCの総合的なつながりの強さを求めます。
専門用語を使うと、統計力学で使われるグリーン関数という量を使って相関の強さを計算しました。例えば、物質の中で動き回っている電子は、別の電子にぶつかり、さらに他の電子に影響するというように相互的に作用しています。このような相互作用する電子を介した相関の程度を計算するときに使われるのがグリーン関数です。
これをザッカリーの空手クラブの複雑ネットワークに応用し、リンクを繋げ直しました。ある2つの点の間のグリーン関数（相関の強さ）が一定値以上であれば、その2点がたとえもとは繫がっていなかったとしてもリンクを繋げます。一方、グリーン関数が一定値より小さければ、その2点がたとえもとは繫がっていたとしても、リンクを消してしまいます。このような手順でリンクを繋げ直した結果、図3のようになりました。明確に2つのコミュニティーが検出できています。これはザッカリーの第2の質問とばっちり一致していて、答え合わせに成功しました。

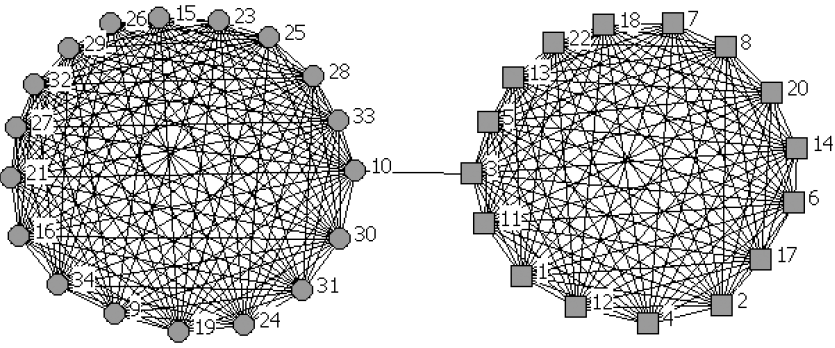
図3 「ザッカリーの空手クラブ」を我々のアルゴリズムで繋ぎ直したネットワーク

ところで図3では3番と10番が2つの派閥を橋渡しする「希望」であることもわかります。このようにコミュニティーの橋渡し役がわかる点も、我々のアルゴリズムの特徴の1つです。従来の方法では多くの場合、ネットワーク全体を完全に2つに分けてしまい、橋渡しを検出できずにいました。
この手法を用い、アメリカの空港のネットワークでも、コミュニティーの検出に成功しました。その結果、東部と中西部の2つのグループがあり、それらをシカゴ空港とアトランタ空港が橋渡ししていることもわかりました。

メールのやりとりだけで海外の研究者との共同研究を完成させる

実はこれまで、このような統計力学の考え方に基づいたアルゴリズムで、複雑ネットワークを考えるということはほとんど行われてきませんでした。「ザッカリーの空手クラブ」も数学的な手法では分析されていましたが、物理の手法を使ったものはありませんでした。
研究のきっかけは、20年ほど前、キューバ出身の研究者で、スペイン在住のエルネスト・エストラーダさんという方から連絡をいただいたことでした。
彼は数学的手法によるネットワーク解析の専門家です。当時、複雑ネットワークの研究が始まったところで、物理的な解析手法を使った私の研究に興味を持ってくださいました。そしてメールのやりとりだけで、彼と共著の論文が1本完成しました。その後、直接お目にかかったのは、彼を日本に招待した数年後のことでした。

統計力学はなぜ生まれたか

ここまでご紹介してきたように、統計力学の手法を用いて複雑ネットワークを効率的に解析できました。それは、統計力学が多数の物が集まった時に起こる現象を解析するのに優れた手法だからです。そのような統計力学が物理の歴史のなかでどのように生まれたか、おそらく一般の方にはあまりなじみのないこの学問について、簡単にご紹介したいと思います。
物理学は要素還元主義から始まりました。要素還元主義というのは、つまり、世界を分子や原子、さらには原子核と電子、素粒子などと、細かく見ていくことによって、全体の法則性を見いだそうという考え方です。
これはキリスト教などの一神教とも関係しています。神様がこの世界を作ったのだから、世界を細かく見ていくことで、そこにさまざまな法則性が隠れているのを発見できるはずだと考えられていました。
一方、18世紀半ばから19世紀に産業革命が起きると、物理の一分野に熱力学という学問が生まれました。これは蒸気機関車のエンジンのような大きなものを対象とし、どうすれば効率よく熱機関を動かせるかについて考えることを目的としていました。
しかし、ガスの気体の粒子のふるまいがわかっても、それだけではエンジンのような大きなものを効率よく動かす方法はわかりません。効率化に関連する圧力や温度がどのようなものかを説明する必要があります。
そこで、従来の微視的な学問と、熱力学のような巨視的な学問を結び付ける、つまり多数の粒子の運動、圧力や温度、エントロピーなどの熱力学の性質を、微視的な法則から説明する学問として生まれたのが統計力学でした。これが20世紀の初め頃のことです。20世紀後半に入った頃に、ものがたくさん集まった時に初めて現れる全く新しい普遍的法則を統計力学が見つけました。これは物理学を要素還元主義とは全く違う方向に向けました。一神教から八百万の神の世界に向かっていると言えるかも知れません。
このように、統計力学は、ものがたくさん集まった時に起こる現象を、統計的な手法で扱います。ものの集まり方には無数の組み合わせがあります。そうした特徴から応用範囲が広がり、21世紀に入る頃には人間や社会などのネットワークや、為替変動のダイナミクスを統計的に説明するためにも使われるようになりました。そのような流れから上述の研究が生まれました。

量子力学の金科玉条への挑戦

さて次に、私のもう1つのテーマである量子力学の研究についても、ご紹介したいと思います。
物理学というと、多くの方は、素粒子や宇宙などの研究をイメージするかもしれません。しかしこうした分野の研究は、実験に非常にお金がかかり、一部の大きな研究機関でなければできないため、研究者の数は限られます。いま、多くの物理研究者は、物性物理という領域の研究を行っています。物性物理学では、量子力学や上述の統計力学を中心とした物理の考え方や手法にもとづき、物質の性質やふるまいを研究します。
私が取り組む量子力学の研究領域のキーワードは「非エルミート性」です。これを説明するために、まず一般的に大学で習う量子力学がどういうものかをお話しします。それは外と全く何も関わりがない閉じられた系（システム）のなかに量子的なものがあると想定し、それらがどのように運動しているかを考える学問です。
この閉じた系の中ではエネルギーは保存され、外とやりとりすることはありません。また、粒子数も保存されています。それはつまり「一定である」ということを意味しています。大まかに言うと、この「ずっと永遠に変わらない」という性質をエルミート性と称します。反対に「エルミート性」でないものが「非エルミート性」です。正確な説明ではないのですが、まずそのように理解していただくとわかりやすいのではないかと思います。
教科書で習う量子力学ではこの「エルミート性」が金科玉条となっています。しかし現実の世界では、当然ながら、物質の周りにたくさんのものが存在して、周りとエネルギーや粒子をやりとりしています。実験では、「エルミート性」をできるだけ保つために、物質の周囲を真空にして、なるべく粒子がぶつからないよう、そ～っと測定します。この「そ～っと測る」ことに大変なお金と労力がかけられているのです。
私は「エルミート性」という金科玉条の前提を崩したところに、何か新しい発見があるのではないかと考えました。これが現在取り組んでいる開放量子系の研究の原点です。開放量子系というのは、文字通り、閉じられた世界ではなく、マクロな外界と強く相互作用している時、何が起こるかを考えようという学問です。開放量子系の性質や振る舞いを正確に予想できるようになれば、実験で「そ～っと測る」必要がなくなります。これは物理学に大きな変革を生むのではないかと期待しているのです。

新たな理論の原点を創造する

開放量子系の着想に至るまでには、試行錯誤がありました。一番初めに非エルミート性を応用した研究は、開放量子系とは異なる分野で、研究の対象は局在現象でした。
局在というのは空間的に広がっていけない状態のことです。金属中に不純物を徐々に増やしていくと、ある濃度に達したところで絶縁体になります。つまり、電子の流れが不純物に邪魔されて伝導できなくなります。これは電子が不純物にトラップされて「局在」しているからです。電子波が「局在」するかどうかは、不純物の濃度と電子波のエネルギーに依ります。また、局在している場合にも、どれくらい強く局在しているかを知る必要があります。しかし、実際に電子波の状態を計算してどれくらい強く局在しているかを理論的に調べるのは容易ではありません。
私が着目したのが非エルミート性でした。局在している電子を一方向に押し流そうとするように仮想的に非エルミート性を加えます。非エルミート性を徐々に増やしていくと、あるところで局在していた電子が動き出します。電子が動き出した時を理論的に検出するのが実は容易なのです。そこで、どれくらいの非エルミート性を加えたところで電子が動き出したかを検出すると、非エルミート性を加える前にどれくらい強く局在しているかを簡単に知ることができるのです。
これはちょうど、虚数（英語では「想像上の数」）を導入すると実数の世界をより深く知ることができるということと似ています。虚数を導入することで初めて負の実数さえ平方根をとることができるようになりました。
私がこの成果を発表した1996年当時、このように非エルミート性に着目した研究はほとんどありませんでした。その後、この研究から非エルミート量子力学という新しい学問が生まれました。今では私が導入した非エルミート・モデルは共同研究者で恩師の先生の名前と私の名前をとってHatano-Nelson模型と呼ばれ、非エルミート量子力学の原点となるようなモデルと認めていただけるようになりました。

羽田野直道氏

常識の裏をかく研究

Hatano-Nelson模型は「常識の裏をかく」ことで実現しました。この体験を通して、他の人がやっていない、常識を変えるような研究の面白さを知りました。そこで次に、行った研究が上述の開放量子系です。ただ、移行は簡単ではありませんでした。
最初に、開放量子系に着目したきっかけは、原子核にも非エルミート性が現れることを知ったことです。現象として面白そうだと興味を持ったものの、電流の局在とは学問体系が全く異なります。いろいろ勉強しなくてはなりませんし、他の研究者が面白いと思うような問題設定をなかなか思いつくことができませんでした。論文を書けない時期が2、3年間続きました。
「開放量子系」をキーワードとする問題設定にたどり着き、最初の論文を発表したのは、2001年か2002年頃だったと思います。それまで、研究者の間で「開放量子系」ということばは使われていないわけではありませんでしたが、このような問題設定で1つの学問にしようと試みたのは、私の研究が初めてです。
この研究はまだ始まったばかりです。物理領域の研究者はもともと、装置の中の「閉じられた系」での測定に慣れています。このため、外と強く相互作用する開放量子系の学問の発展によって、実験が非常に簡単になるということは意識されていません。これは、未然課題と言えるのではないかと思います。
しかし、それまでの研究を振り返れば、Hatano-Nelson模型の研究を始めた当初も、「誰もやっていない」という点では同様でした。「非エルミート性が面白そうだ」と言う研究者はいても、実際に研究をする人はいませんでした。
あれから約25年。現在、非エルミート量子力学は徐々に世界の研究のキーワードになりつつあります。「非エルミート量子力学でこういうことができる」という論文も、ようやく増えてきたところです。
開放量子系でも大きな変革をもたらしたいと考えています。今はまだ、どのようにしたら実現できるかわかりませんが、わからないこと自体が研究の醍醐味とも言えるのではないでしょうか。

研究者は「博打（ばくち）打ち」であれ！

以上が、私の研究室で行っている研究テーマの一部の紹介です。
これらの研究を通して、1つ強調したいことがあります。それは研究とは、新しい分野を作ることだということです。私がハーバード大学でHatano-Nelson 模型の研究を始めたとき、一番感じたことは、ここではみんなが自分で新しい分野を作ろうとしているということでした。
それまで日本の大学院でやっていたことを振り返ると、すでに研究者の間で問題だと認識されていることをみんなで一緒に研究し、成果を競っているにすぎませんでした。特に能力のある人は、「自分のほうができる」と考え、既存の問題の競争に加わりがちです。
ところがハーバード大学ではそうではありませんでした。新しい問題や新しい分野を作ることをみんなが目指していました。やはり、研究者はそうでなければいけないと強く感じました。私が、「非」とつくテーマに取り組むようになったのはこの時からです。「非エルミート性」をキーワードとする研究もここから始まりました。
今は研究室の院生にも、自分で問題を考え、他でやっていないテーマに取り組むよう指導しています。時には私が知らないようなテーマをやりたいという学生もいます。そういう時は「自分で勉強して僕に教えて」と話しています。このため、研究室では非常に幅広い研究テーマを扱っています。
自分で考えた問題に取り組むというのは、良い点と悪い点があります。良い点はもちろん、自分で答えを出すことができれば、世界で初めて自分が解いたオリジナルの研究になることです。
一方、大変な点は、自分は面白いと思っても、その問題を他の人も面白いと感じるか、自分が解いた答えを面白いと受け止めてもらえるかわからないことです。ですから、やっている間は非常に不安です。でもそれも研究の一部なので、我慢して進めるしかありません。
私は、研究者は「博打打ち」でなければいけないと思っています。
つまり、自分が面白いと思ったことは、きちんと説明すれば、きっと他の人も面白いと思ってくれるに違いないと信じ、そこにかけるしかないということです。それができなければ、結局、怖いからやめよう、みんながやっている問題をやろうとなってしまいます。それでは新しいことは生み出せません。
恐れや不安に向き合い、博打を打ち、とことん考え抜くことで、新しい学問分野を作っていくことができるのだと考えています。

羽田野研究室：http://hatano-lab.iis.u-tokyo.ac.jp/index-j.html

（2023年2月24日 東京大学生産技術研究所羽田野研究室において　取材・構成：田中奈美）