数式を道具に、循環する社会の実現を研究する（下）｜本間裕大

「未然課題」連続インタビュープロジェクト

インタビュー#19　本間 裕大

東京大学生産技術研究所 准教授｜数理最適化モデリング

観光客に便利で地元の人の防災拠点にもなる「道の駅」の最適配置とは？　歴史的な街並みが残る川越市一番街の、観光客と住民が共存できる歩行者天国とは？　お互いに視界に入ることで交流を生むパブリックな可視空間とは？
数理モデルを用いてそんな「人間模様」の本質を表現する本間裕大氏は、数式を道具に循環する社会を実現するための研究をしています。社会と個人にとっての「最適化」とは何か、そしてその背景にある未然課題についてうかがいました。前編に引き続き、後編をお届けします。
＜前編：https://oec.iis.u-tokyo.ac.jp/topics/186/＞

社会の課題を解く鍵はバランス

前編で「最適」とは何かということを述べました。結局、社会はすべてバランスではないかと私は考えています。
例えば川越市の交通政策を分析するプロジェクトでは、歴史的町並みが残る一番街の歩行者天国化について、詳細な交通シミュレーションを行い、規制をしなかった場合、一方通行にした場合、歩行所天国にした場合を分析して、安全と利便性が両立するよう、そのメリットとデメリットを整理しました。
こうした交通を読み解く鍵がまさにバランスです。車が集まれば渋滞が増えて速度が落ちます。するとそこには車が集まらなくなるので車が減ります。つまり、通過する所要時間や速度が人の経路選択行動を決め、その経路選択行動が所要時間や速度を決めるという相互連関構造が成立しています。それらを考慮し、あらゆる移動の可能性のなかでちょうどよいバランスが取れる状態を分析しました。
また、2021年と2022年には、全国の中高生を対象とした「飛行機ワークショップ」で、私たちが開発したシミュレーションソフトを使って、経済と環境の両面を考慮した航空線路を考えてもらうという機会がありました。
参加者の中高生には、環境にやさしいが価格の高い燃料をどの程度使うかなど、いくつかの制約条件のもとで、具体的に世界の都市を結ぶ航空路線を考えてもらい、発表してもらいました。社会のバランスの難しさを体験することができたのではないかと思います。
なおこの企画は、東大生研次世代育成オフィス（ONG）と日本航空が共同で行っているSTEAM教育の一環で、私が代表を務めた2020年と2021年の企画チームは2022年3月に、日本オペレーションズ・リサーチ学会で、第48回・普及賞を受賞しました。

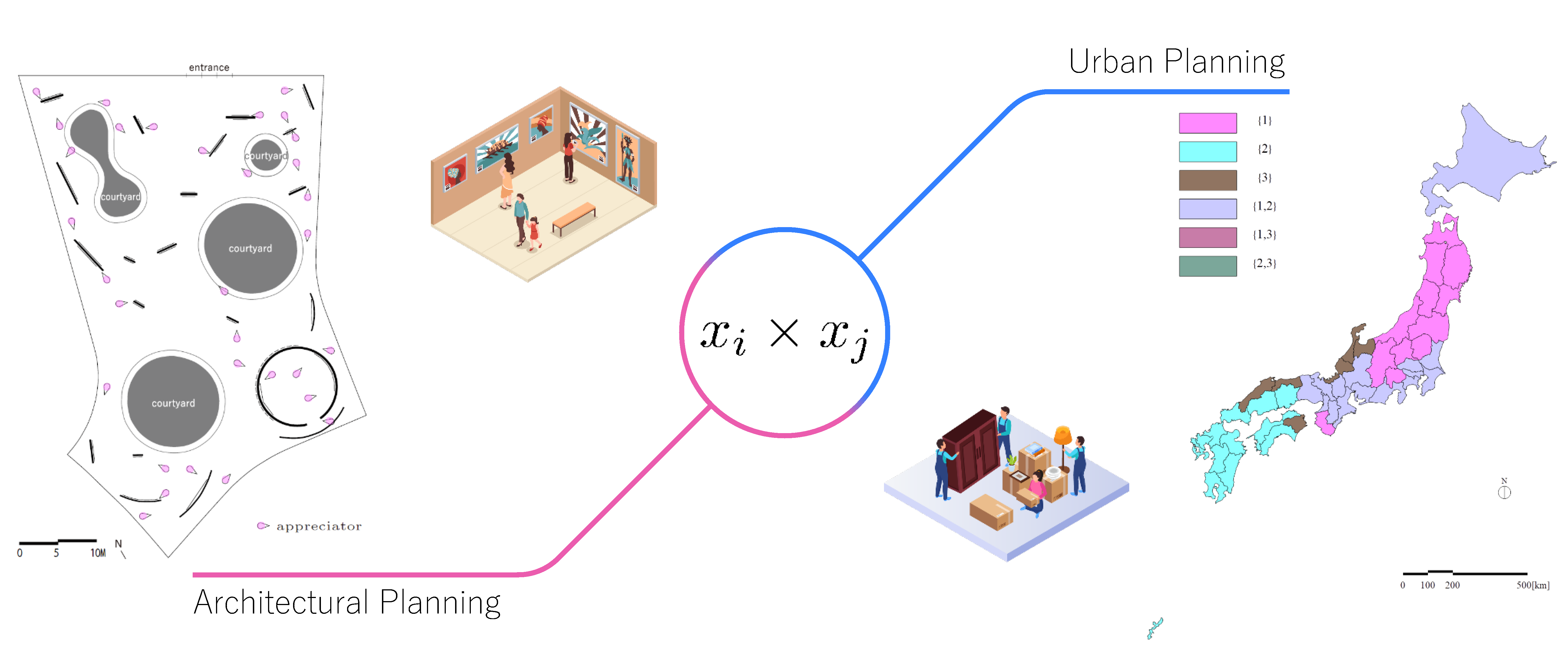
社会システムを考える上で重要な「xi（わたし）×xj（あなた）」の関係

社会のバランスという点でもう1つ、私たちの社会システムはインタラクティブな交流によって決まると考えています。つまり、自分の意思決定と相手の意思決定の掛け合わせによって初めて決まるということです。
こうした「人間模様」の本質を表現する数理モデルの一つに、2次式≒掛け算が挙げられます。言わば、自身（xi）と他者（xj）との繋がりによる相乗効果（xi × xj）を考えるわけです。
少し混んでいる美術館を想像してください。ある絵画の前に「立つ」を1、「立たない」を0で表現することにしましょう。このとき、仮に私が絵画の前に立っていても（xi=1）、他の方が同じ絵画の前にいなければ（xj=0）、1×0=0で「ぶつからない」わけです。しかし、もし他の方も絵画の前に立とうとすると（xj=1）、1×1=1で「ぶつかる」ことになりますね。
道の駅のように、片方が人、もう片方が施設の場合、このようなファクターはあまり強く見えてきません。しかし、美術館で、みんなが絵画を鑑賞しやすいよう譲り合って立つための最適配置を考えると、「自分がこう動き、それに対して相手がこう動く」という相互交流のファクターが強く結果に影響します。
この例には、価値観の話も含まれています。そもそも人はどのような状況で快適あるいは不快だと感じるかということを、丁寧に考える必要があります。たとえば自分が「モナ・リザ」の絵の目の前に立ち、他の人は視線に入らない状況で、じっくり鑑賞することができたとしても、後ろにたくさん人が並んでいて、その冷たい視線を感じていた場合、本当に快適だと言えるでしょうか。
ですから、自分からは人が見えないパターン、自分が人から見られないパターン、双方に視界に入らないパターンなどさまざまな状況を考慮し、自分の視界に入るという総和を最小化した場合、あるいは人から見られないという総和を最小化した場合のように、両極端な結果を比較しながら、バランスを考えていくことが重要です。これは社会システムについて考えるときにも同様だと思います。

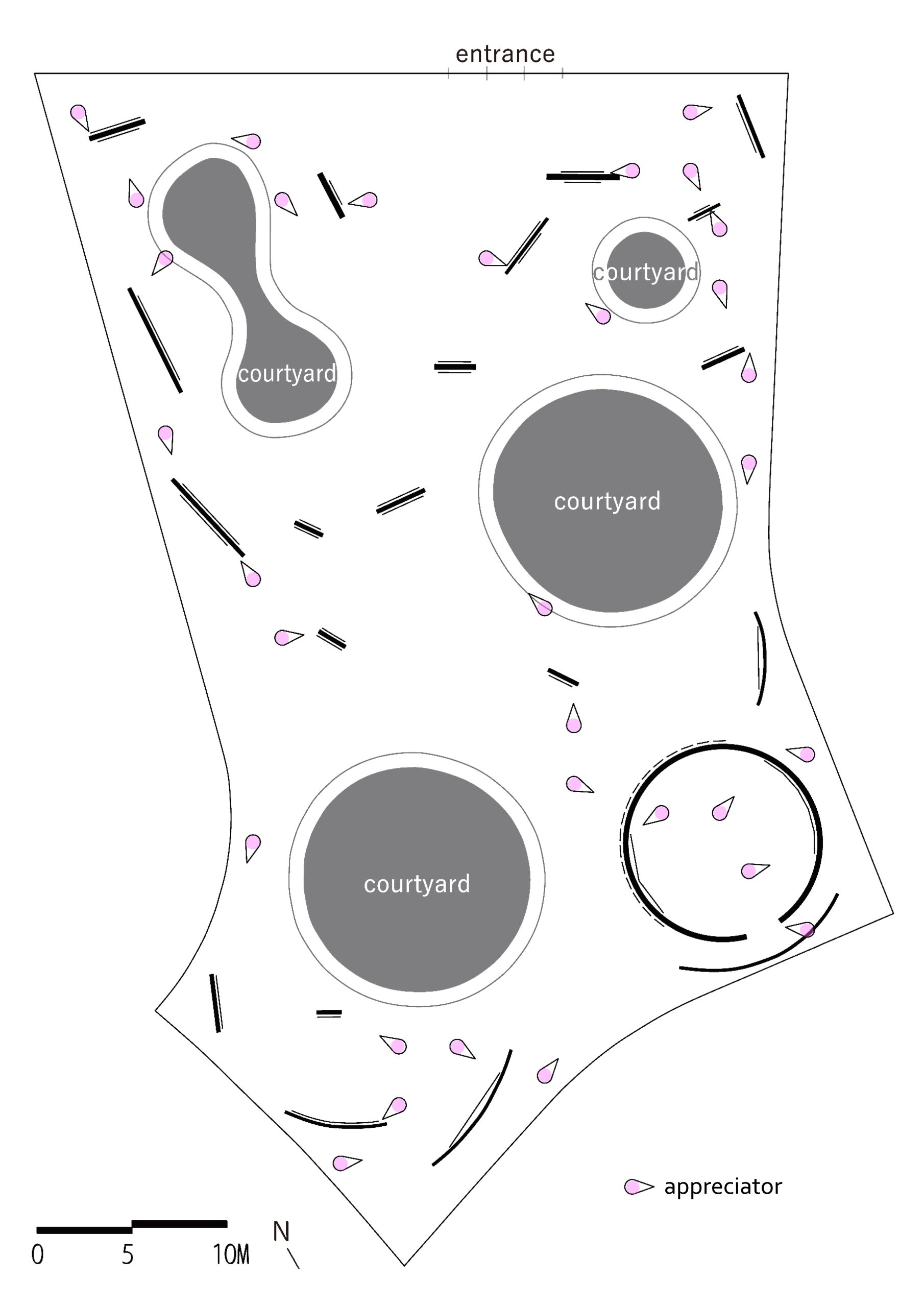
軽井沢千住博美術館で、同じ空間にいるすべての鑑賞者が、誰も視界に入らず、誰にも見られない状況で、同時に何人が鑑賞できるか計算すると、最大32人という結果だった。

たくさんの研究の種を蒔く

このほかにもこれまで、学生ピアノコンペティションの時系列採点データを活用した、戦後日本社会におけるピアノ教育過程の数理分析、花火がどのくらいの大きさで、かつどのくらいの割合で視界にとらえられるかを定量的に評価する研究、「ファッションプレス」との共同で、有名ブランドが発表するコレクション写真データを活用したトレンド分析など、さまざまなテーマに取り組んできました。
余談となりますが、トレンド分析に用いている数理モデルは最適配置のモデルです。充電ステーションでも道の駅でも、最適配置を分析するというのは、人の分布をいくつかのクラスターに分け、そのクラスターごとの「真ん中」を探す作業となります。
ファッションでもたくさんの分布の中からグループ分けをして、それらの中心を探し、各年度で比較することで、どこの中心が動いているか、どのグループがどこへ移動して、どのグループが大きくなっているかなどがわかります。
なぜ、これだけさまざまなテーマがあるかというと、私の研究室では修士の学生に、自分たちの好きなテーマを探してもらうということを徹底しているからです。自分だけが種を蒔いていると、同じことばかりやるようになってしまうので、最初の種を学生にまいてもらうようにしています。
そうして育ってきたプロジェクトも多く、その1つに、凸空間システムの開発があります。これはもともと、修士の学生が形の複雑さを定量的に評価する新しい手法を作りたいと提案してきたことがきっかけになりました。
実はこのアルゴリズムというのは、数学的に極めて煩雑です。学生が卒業したあと、そのまま眠らせるのはもったいないということで、株式会社セックに入っていただき、凸空間列挙システム「Convex Space Visualizer」を開発しました。これは誰もが使える空間解析システムとして、GitHubで無償公開し、その成果は学会でも発表しました。
実はこの研究は、上述の美術館における最適鑑賞位置とも関連しています。美術館の場合、どうしたらお互いを見ずにすむかというプライベートに関する課題でしたが、一方で、凸空間はお互いに視界に入ることで交流を生むパブリックな可視空間が課題です。
例えば下の図ではAの人は、B、C、D、Eすべての人を見ることができますが、BとC、DとEの人はお互いを見ることができません。Aを中心とした主従関係のような空間となっています。
では、交流を生む建築空間とはどういうものか考えたとき、それはみんなが一体感を感じ取れる空間です。そしてそれは空間の中にいるすべての人が、どの場所の２人を取り出してもお互いを見える関係が成り立っている空間だと考えることができます。それが下の右図の緑部分のような窪みがない空間です。

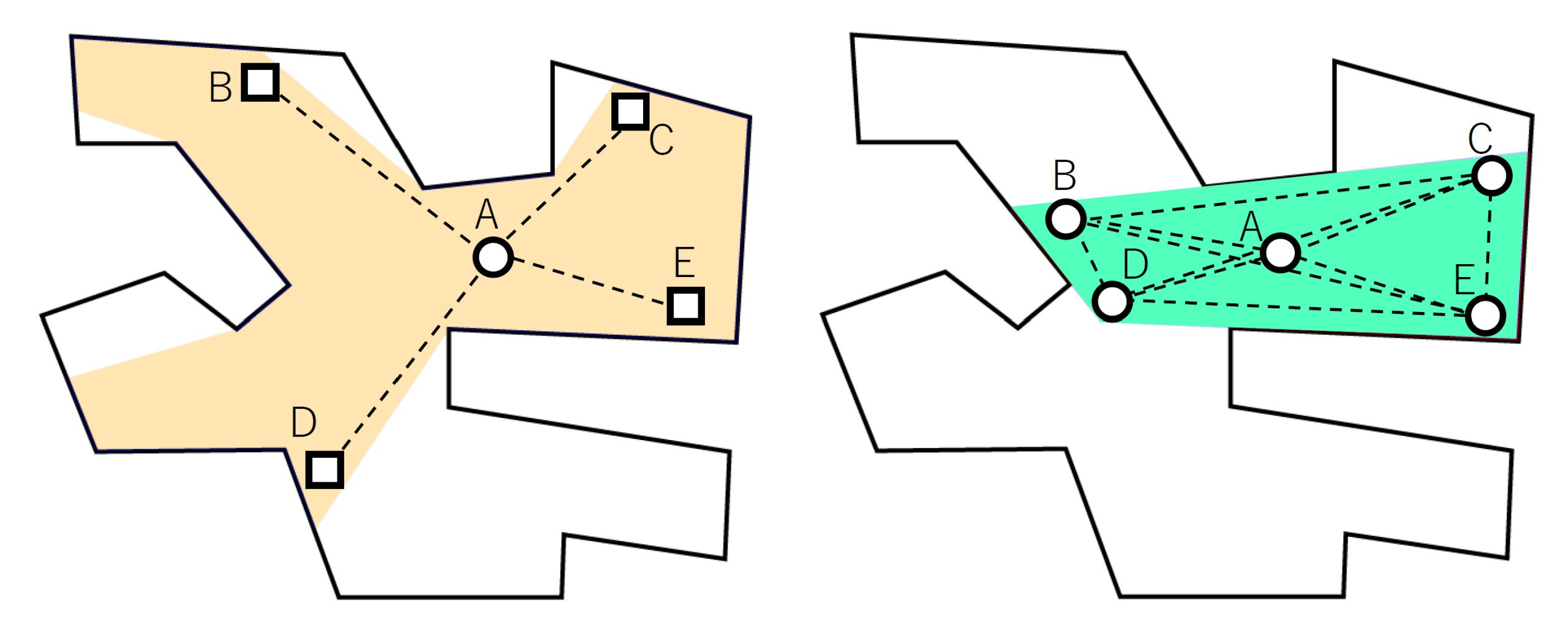
左：主従関係のある空間
右：窪みがない空間

さらに数学的に窪みのない空間とはどのようなものを考えると、この場合、重要なことはxi × xjのインタラクティブ交流が成立すること、さらに1対1だけではなく、その場にいる全員が対等に交流しあえるような空間に最適化することです。
このような空間の「最適化」の道筋は、すでに技術的には確立しています。今後は上述のソフトウェアを一層深化させ、例えば最も面積の広い空間、最も丸い空間、最も壁に接している空間など、どのような最適化基準でも柔軟に対応でき、より多様な空間設計業務へ活用できるようなソフトウェア開発を、セックとともに進めているところです。

個人と社会システムにおける最適化のバランス

私が取り組んできた研究を通して未然課題を考えると、それは、社会全体の最適と個人の最適化が、多くの場合、相反するものだということではないかと思います。みんなが自分のためだけに最適化しようとすると社会全体のバランスが悪くなりますし、社会全体だけで最適化を考えると、個人の自由や権利が阻害されかねません。これもまたバランスが重要で、長期的に考えなければならない問題だと感じています。
ではそのバランスとは何かを突き詰めて考えたとき、21世紀のいま、社会主義が崩壊したとしても、資本主義で本当によかったと思う人はあまり多くないのではないでしょうか。そうすると、資本主義でも社会主義でもない中間のシステムは何かということになります。私が理想として考えていることは、個人が最適行動をした結果が、社会の最適になるような仕組みを作ることができないかということです。
これまでの研究で、私は「都市・社会を数学の力を使ってより良い状態に導く」ということを考えてきました。そのためには冒頭で述べたような「デッサン力」が必要です。そしてそれを養うには、理論や技術を身に付け、試行錯誤しながら何度も練習を繰り返すしかありません。
美術館の最適鑑賞配置や凸空間システムの開発も、あのようなデッサンを思いつくまでに、実は1年近くかかっています。最初は立っている人から視線のビームを出し、そのビームが集まったところにヒートマップかけてみるという方法を考えました。
しかしある先生から、「視線がぶつかってもエネルギーが発生するわけでもないし、ヒートアップに何か意味があるか？」とご指摘いただいて、冷静に考えれば、その通りだと思い、いまの研究へと繋がりました。
確かに「とにかく多くのデータを取得し、コンピュータを最大限に活用すれば、現実の良い近似となる」ことはわかるのですが、本質を取りきれてない、自分の中のもやもや感が残ります。このもやもや感がなくなり、完全にきれいな輪郭と骨格が描けるということが、デッサンをするということだと思っています。
このように練習を重ね、数理モデリングのデッサン力を高め、より良い建築・都市計画へと結びつけるための可能性を探求してゆきたいと考えています。

本間研究所：http://www.honma-lab.iis.u-tokyo.ac.jp/
Convex Space Visualizer，GitHub（2022年9月14日公開）：https://github.com/sec-archispace/ConvexSpaceVisualizer

（2023年2月10日 東京大学生産技術研究所 本間研究室において　取材・構成：田中奈美）